when the body changes it’s position with respect to reference point and time than body is said to be in motion. Motion can be of different type depends upon the path adopted i) Circulatory Motion which have a circular path ii) Linear motion when body moves in straight line iii) Oscillatory/ vibratory motion when a body moves in to and froth path.
PHYSICAL QUANTITY There are seven basic physical quantities ie length, time, mass, temperature , amount of substance , electric current and luminous intensity they have both magnitude and unit but they are classified in two groups a) Scalar quantity the physical quantity having only magnitude such as length, mass, time b) vector quantity is that physical quantity which have both magnitude and direction such as displacement , velocity , force weight
DIFFERENCE BETWEEN DISTANCE AND DISPLACEMENT :
Distance is the length of path travelled by the body whereas displacement is the shortest distance between initial and final position of the body
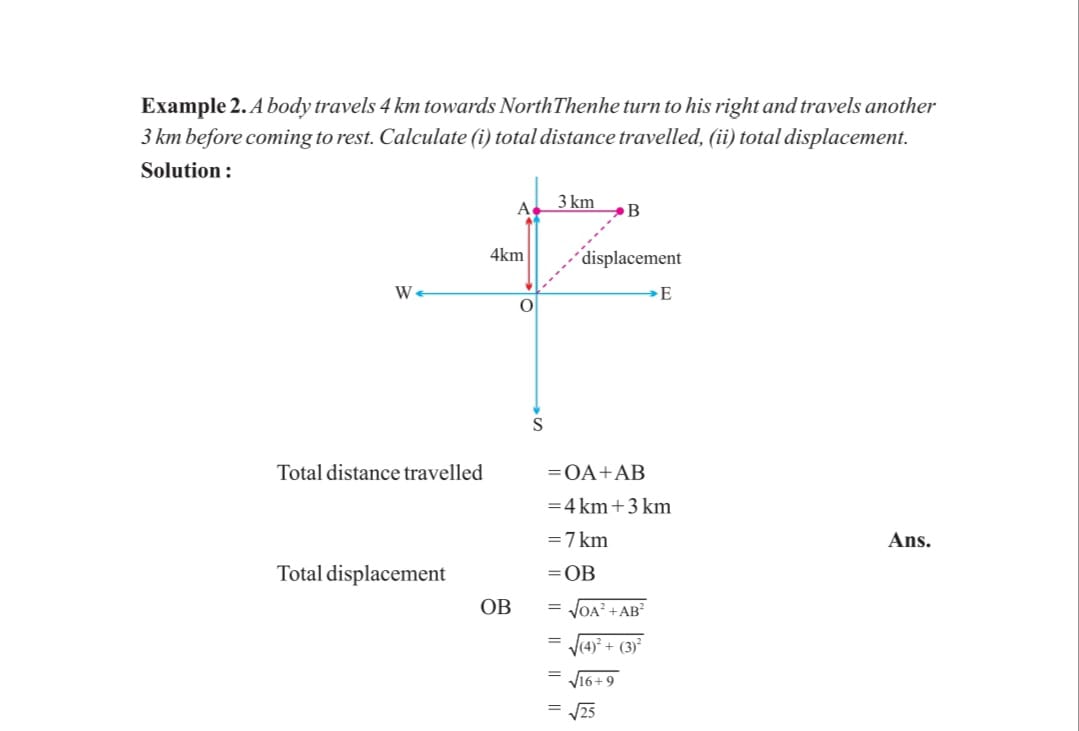
( examples taken from support material NCT )
UNIFOM MOTION : When a body travels equal distance in equal interval of time example movement of hands of the clock .or a person travel 2 meter in first second, again 2 meters in next second and so on .
NON UNIFORM MOTION : When a body travels unequal distance in equal intervals of time such as in first a person walks 3 meters than in second he walks 4 meters than in third second he travels 2 meters
SPEED : The distance travelled by body in unit time is called speed. It is scalar quantity unit SI meter/ second or Km/ hr Speed = distance/ time If body is moving in uniform motion than the speed is constant but in non uniform motion the speed is not same average speed can be calculated as Total distance travelled in journey divided by total time taken in journey. Average Speed = Total Distance Travelled / Total time taken
Example : What will be the speed of the body in m/s and km/hr if body travel 60 kms in 6hrs
speed = distance /time = 60/6= 10 km/hr
in m/s (multiply km/hr by 5/18 = speed in m/s) so 10×5/18= 50/18=25/9 m/sec
VELOCITY : The speed of the moving body in given specific direction is called velocity . It is a vector quantity Its value changes either magnitude or direction changes SI unit meter/ second.
AVERAGE VELOCITY It is the mean value of initial velocity (u) and final velocity (v)
Average velocity = (u + v) /2
Example : During first half of a journey a body travels with the speed of 40 km/hr and next half it travels with the speed of 20km/hr than the average speed is
40+20 = 60 >>> 60/2= 30 km/hr
Example if a car travels 20km in first hour 60 km in second hour and 40 km in the third hour than average speed =( 20+60+40) -:- 3= 120 km /3 = 40 km/hr
ACCELERATION : It is the rate of change of velocity is called acceleration .
Acceleration = (Final velocity – initial velocity)- -: –_ Time In this case v>u
a= (v-u) / t SI unit meter/ second^2
RETARDATION/ DEACCELERATION : The rate of decrease in velocity is called deacceleration that is change in velocity -:- time it is also called negative velocity SI unit meter/ sec^2 In this case u>v
Examples : a) A car is travelling with the speed of 40 km/hr increases to 70 km/hr in 5 sec than acceleration of car = change in speed = 70-40 = 30 km/hr
change in speed in m/s = 30 x5/18 = 5×5/3= 25/3 acceleration = change in speed -;- time
25/3-;- 5 = 5/3 meter/ sec^2
example b) If a car is moving with the speed of 20 km/hr comes to rest in .5 hr than the retardation is = 0-20 = -20 km/hr now
time taken ‘5 hr than deacceleration = change in speed -;- time = -20 -;- .5 = 40 km/hr^2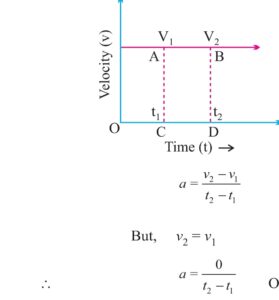
At constant velocity acceleration is Zero
Velocity increases create the accelerate a=( v2- v1) -:- (t2-t1)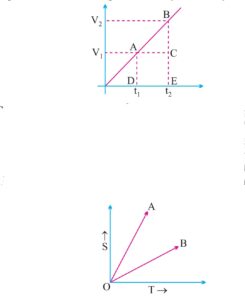
ii) Body A has more velocity as slope is more
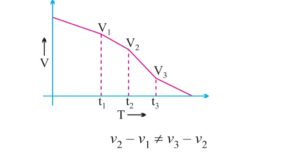This graph represent deacceleration
EQUATION OF MOTION :
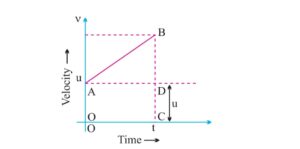Let us suppose a body starts moving with the velocity u at A after time of t seconds it’s velocity becomes v at B . Now by graph change in velocity is BC -DC = BD====> V-U time taken = OC = t
Acceleration = change in velocity / time =====> a = (V-U)/t===> at = V-U ====> V= U+ at
first equation of motion is ==== > v= u +at
Total distance travelled (S) as we know that average velocity =( Initial velocity + Final velocity )/2
total distance travelled = average velocity x time = => equal to aera of the given figure OABDCO which is trapezium whose aera = 1/2x( sum of parallel sides ) height ==> sum of parallel sides = OA+BC =(u+v ) height=OC= t
S= 1/2 x (v+u ) t ====> put the value of v=u+at S= 1/2x(u+at+ u) = 1/2 (2u + at)t
S= ut + 1/2 at^2 (second equation of motion )
as we know that distance travelled= area of given figure OABDCO = S= (V+U) t/2 put the value of t from equation first ===> v= u+at ==> t=( v-u)/a
S = (v+ u) (v-u)/2a ====> 2aS = (v+u) (v-u)====> 2as = V^2 -U^2 ==> U^2 + 2aS = V^2
v^2 = U^2 + 2aS ( third equation of motion )
Example a) A car starting from rest moves with uniform speed with acceleration of 0.2 m/s^2 foe 4 minutes than the speed (1st equation ) v= u+at v=? u=0 t = 4×60 = 240 sec than V=0+0.2×240 = 48 m/s and distance travelled S = ut+ 1/2at^2 = 0x240 + 1/2 x0.2×240 = 0 +24= 24 meters
b)When is applied to car it produces deacceleration of 6m/s^2 opposite to the direction of motion if it stops in 2 sec than the distance travelled will be S= ut + 1/2 at^2 first we have to find u =? as body stops therefore v=0
V= U- at ==> 0 = U – 6×2 ==> u= 12 now in the second equation s=12×2 – 1/2x6x2x2 = 24-12 = 12 meter
UNIFORM CIRCULAR MOTION If the bodyis moving in circular path with uniform speed it’s motion is called uniform circular motion. In such kind of motion speed reamin same but direction changes every moment so it produce an acceleration during the circular motion velocity = 2xn r/t (n= pie = 2/7)